AXEL

En nuestro Blog podrás encontrar información acerca de la Teoría de Conjuntos y Teoría de Grafos. Esperamos que te sea de mucha utilidad.

INTRODUCCIÓN:

En este trabajo se tratará de explicar lo que son los grafos y conjuntos, sus tipos, y algunas derivaciones de ellos, así como su representación gráfica y en algunos casos, su representación en algún programa informático.

• Teoría de Conjuntos: Con ella se entiende mejor la lógica matemática, la matemática combinatoria, la especificación de lenguajes de programación y la teoría de autómatas y computación. 
• Teoría de Grafos: En esta se basan muchas de las técnicas avanzadas de programación.

La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades y relaciones de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.

Hipótesis del continuo. La colección de todos los conjuntos de números naturales P(N) tiene la llamada potencia del continuo: tantos las funciones como (por ejemplo) puntos en una recta. Su estudio es uno de los principales problemas en la teoría de conjuntos.

Para representar un conjunto de forma textual, se delimitan los elementos entre llaves y lo llamamos con una letra mayúscula. de la forma: A={elementos}

Los elementos de un conjunto pueden describirse de dos formas:

• En extensión o lista:Por la expresión todos los elementos separados por una coma: A={a,b,c,d}
• Por Comprensión:Por la declaracion formal de una propiedad que cumple todos y cada uno de sus elementos: A{a/p(a)}

Álgebra de conjuntos.

Existen unas operaciones básicas que permiten manipular los conjuntos y sus elementos, similares a las operaciones aritméticas, constituyendo el álgebra de conjuntos:

• Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene cada elemento que está por lo menos en uno de ellos. 
• Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B. 
• Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B. 
• Complemento. El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos (respecto de algún conjunto referencial) que no pertenecen a A. 
• Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez. 
• Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento a pertenece aA y su segundo elemento b pertenece a B.

Los grafos son el objeto de estudio de esta rama de las matemáticas. Arriba el grafo pez, en medio el grafo arco y abajo el grafo dodecaedro.

La teoría de grafos (también llamada teoría de las gráficas) es un campo de estudio de las matemáticas y las ciencias de la computación, que estudia las propiedades de los grafos (también llamadas gráficas, que no se debe confundir con las gráficas que tienen una acepción muy amplia) estructuras que constan de dos partes, el conjunto de vértices, nodos o puntos; y el conjunto de aristas, líneas o lados (edgesen inglés) que pueden ser orientados o no. Por lo tanto también esta conocido como análisis de redes.

La teoría de grafos es una rama de las matemáticas discretas y de las matemáticas aplicadas, y es un tratado que usa diferentes conceptos de diversas áreas como combinatoria, álgebra, probabilidad, geometría de polígonos, aritmética y topología.

Un grafo G es un par ordenado G=(V,E) , donde:
V es un conjunto de vértices o nodos, y E es un conjunto de aristas o arcos, que relacionan estos nodos.

Grafo no dirigido

Grafo no dirigido

Un grafo no dirigido o grafo propiamente dicho es un grafo
G=(V,E) donde:

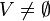
es un conjunto de pares no ordenados de elementos de V.Un par no ordenado es un conjunto de la forma {a,b}, de manera que{a,b}={b,a}. Para los grafos, estos conjuntos pertenecen al conjunto potencia de V, denotado P(V), y son de cardinalidad

Grafo dirigido

Grafo dirigido

Un grafo dirigido o digrafo es un grafo G=(V,E)  donde:

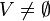
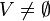
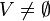
es un conjunto de pares ordenados de elementos de V.
Dada una arista (a,b), a es su nodo inicial y b su nodo final.

Por definición, los grafos dirigidos no contienen bucles.

Un grafo mixto es aquel que se define con la capacidad de poder contener aristas dirigidas y no dirigidas. Tanto los grafos dirigidos como los no dirigidos son casos particulares de este.

Actualmente ha tenido mayor preponderancia en el campo de la informática, las ciencias de la computación y telecomunicaciones.